Protein allostery
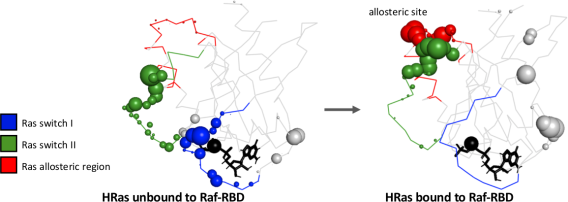
Binding of ligands or complexes far away from the active site can tune protein activity. We are interested in the molecular mechanisms for this information transfer, which could provide design principles for programming biomolecular function. Using atomistic simulations, we extract correlation statistics between dihedral angles to build networks of information flow within proteins. We quantify thermodynamic allostery using the mutual information between dihedrals as well as entire residues. We quantify the kinetic allostery using the conditional activity, a measure of correlation in dynamical activity between dihedrals. We are also building a minimal model to identify necessary and sufficient conditions for focalized long-range information transfer in frustrated materials. Many of these approaches require a computational pipeline to robustly identify discrete configurational states of residues, which we show are well-justified by the clustered distributions of dihedral conformations.
Many proteins are intrinsically disordered, meaning that they exist as an ensemble of different structures. Structural heterogeneity is associated with the formation of small (oligomer) and large (e.g. amyloid fibril) protein assemblies, which play important roles in cell signaling and disease. It is challenging to resolve thermodynamic and kinetic determinants of aggregation fate using existing experimental and computational approaches due to structural heterogeneity and molecular simulation speed, respectively. On the thermodynamic front, we derived an equation for the order-disorder transition of dense polymer melts, which predicts that all protein sequences will (eventually) spontaneously order in the aggregated state. On the kinetic front, we develop conformation-agnostic enhanced sampling methods for MD simulations to determine transition states of oligomers and fibrils of tau and abeta42 peptides, including enforcing conformational symmetry between monomers. We also predicted the transition state of fibril nucleation by generating the structural ensemble of a mutant library and tested the predictions using THT binding kinetics.
Protein aggregation

Physics-based simplification using non-equilibrium circuits
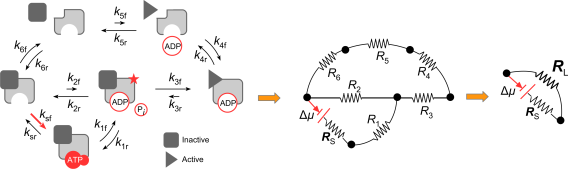
Recently, our lab discovered a mapping from non-equilibrium systems to electronic circuits that obey Ohm’s law. The equation gives the current (flow of matter and information) along any path in the circuit. Transitions that are not directly coupled to the energy source (e.g. ATP binding) are equivalent to resistors in this mapping, enabling systematic coarse graining and design of advanced circuits from the modular composition of simple circuits. We are using this mapping to apply methods and theorems from circuit theory to molecular machines and signaling networks, from which they take on new meaning. For example, we derived a general relation for the efficiency of all chemical engines showing that there is an energy gradient threshold for efficient molecular machines. We are applying this framework to establish general relations between energy usage and information capacity.
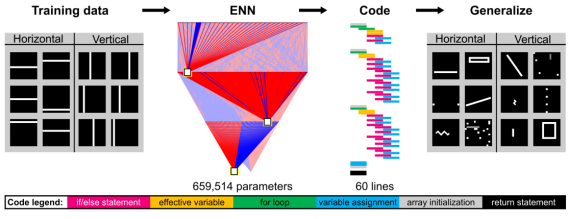
Our lab has pioneered a new class of neural networks, Essence Neural Networks (ENNs), which are trained using a fundamentally distinct algorithm from gradient-descent-based deep learning. Instead, ENN neurons are tasked to draw maximally separating decision boundaries, which feed forward to create more complex maximally separating decision surfaces. This design principle allows ENNs to overcome intrinsic limitations of interpretability and generalizability of deep learning, while maintaining comparative performance on many machine learning tasks. We are exploring the use of ENNs to distill sequence-structure and sequence-function relationships, as well as for protein engineering.
Informatics-based simplification using interpretable neural networks